Charge Transfer in DNA

One thinks of DNA usually as of the carrier of genetic information with quite funny mechanic properties. An interesting and probably unexpected ability of DNA is that it may support the transport of electric charge. This is no theoretical construct but rather a result of experimental observations of numerous researchers. Actually, long-range transfer of electric charge mediated by DNA has been observed and studied in experiments for several years.

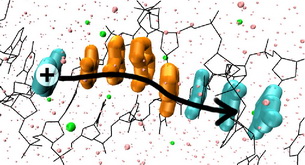
We concentrate on the oxidative charge transfer – that is the transfer of a hole (“missing electron”), which seems to be relevant to radiatively induced DNA damage occurring in organisms, as well as in the repair mechanisms dealing with such damage. This variant of transfer is also the more frequently studied in both experimental and computational research.

The most easily oxidizable part of DNA are the bases, rather than the sugars or even the phosphate groups (although negatively charged). From the deoxyribonucleobases, guanine and adenine have smaller ionization potentials than the others, and this makes them likely charge carriers. Thus, we adopt a chain model of charge transfer in DNA – every guanine and adenine constitutes an element of the chain (dark in the figure):

Now, if we want to study the actual transfer of charge, we need to supply this model with certain parameters. There are two kinds of parameters: site energies, which tell us how attractive every nucleobase is for the charge, are represented by the ionization potentials. The other set of parameters are the electronic couplings, which describe how well the excess charge can be shared by two nucleobases or transferred between them. The parameters may be calculated by quantum chemistry, and a plenty of methods are applicable. Our approach involves the approximative density-functional method SCC-DFTB, which exhibits very good accuracy as well as exceptional efficiency.

It turns out that it would be wrong to consider DNA to be a stationary, frozen cluster of nucleobases and other molecular fragments, placed in a non-interacting medium. The relevant parameters are determined to a crucial extent by the dynamics of the molecular system as well as by the interaction with the solvent. It is thus necessary to take these factors into account in computational studies. Our computational framework is based on molecular dynamics simulations and a hybrid QM/MM implementation within SCC-DFTB.

There are several possibilities to describe the transfer of an excess charge. One is to cast the obtained parameters into the form of a matrix, and set up a Schrödinger equation for the excess charge, where the mentioned matrix works as a Hamiltonian. Of course, the variance of charge-transfer parameters makes the Hamiltonian time dependent. A (numerical) solution of such a Schrödinger equation provides, in principle, the time evolution of the excess charge.

Therefore, once our computational model contains all key elements, we should be able to answer the remaining open questions regarding the transfer: What is the actual microscopic mechanism of charge transfer in DNA? What is the rate of transfer, and how does it depend on the length of DNA strand? What is the effect of solvent exactly like?